Extremely Deviant Yet Normal Drunks

What are the limits of normal behaviour?

It's the end of the night in a town called Luck and a drunk is being sent home from the pub. He only lives 100 steps away in one direction. The pub landlord orients him that way and wishes him all the best.

The drunk takes a unit-sized spatial-step for every unit-sized time-step. He always advances towards his home but he erratically veers perpendicular to his intended direction. He is just as likely to veer left as to veer right. On average, he makes it home but sometimes he ends up quite far away. It is okay if he deviates to the right, he just ends up in a park, but to the left of his home is a lake which he could fall into. This is a daily routine for the pub landlord and recently he's started to worry that his most regular customer is at risk of falling in.

Let Xi be the overall displacement from the perpendicular at time t=i, then:

Xi = Xi-1 + Ui,

where X0=0 and U is the displacement per step. If our hero veers left, u=1; and if he veers right, u=-1. He is just as likely to veer left or right:

P(U=1) = 0.5; P(U=-1) = 0.5.

Figure 1 shows the progress from the pub on a typical night. This time he was lucky and ended up to the right of his home.

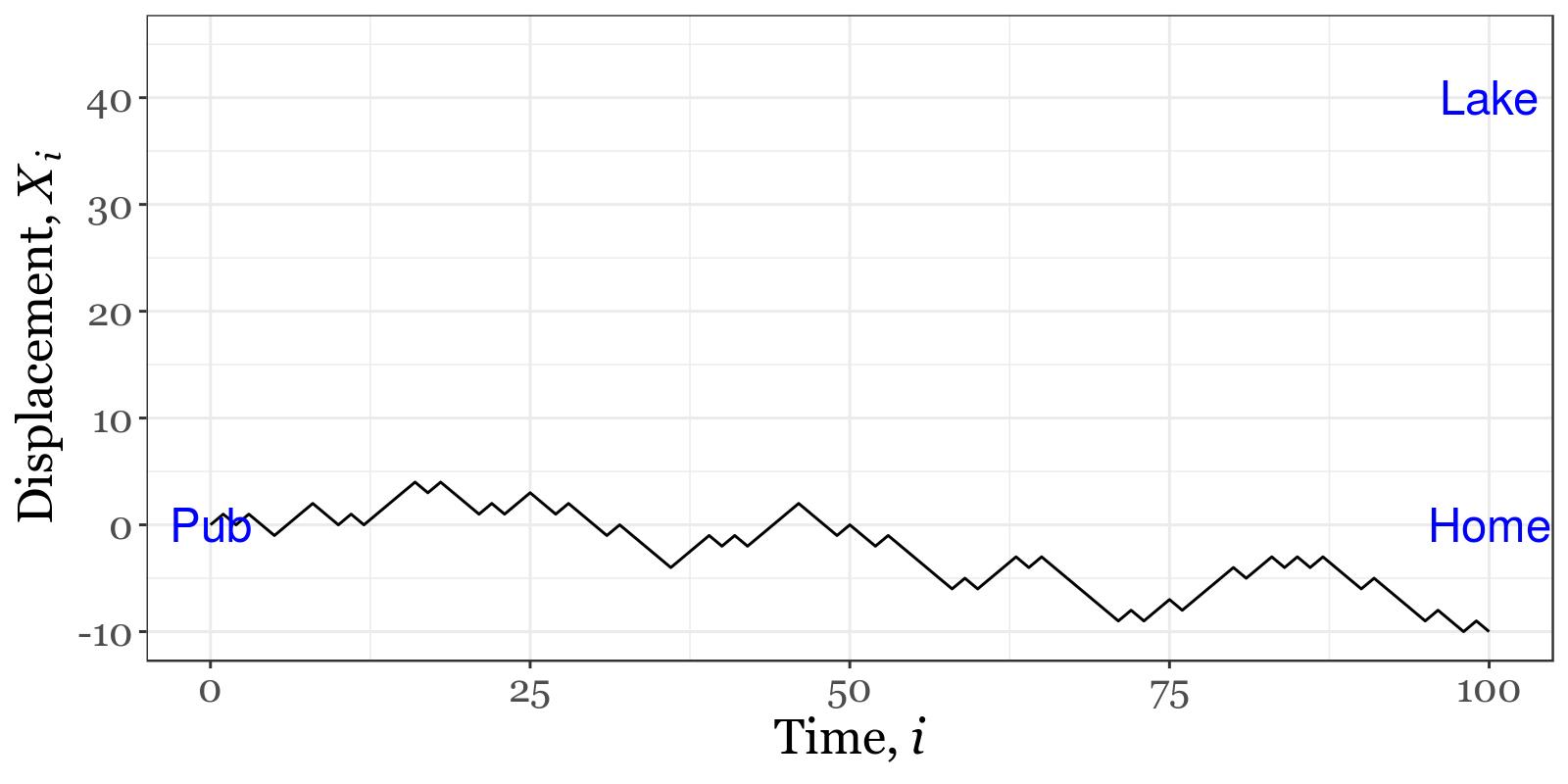
Drunk Displacement Example
Fig. 1: The drunk's progress on a given day showing his perpendicular displacement from his direction home. The positions of pub, home and lake are labelled.
Every day over the course of a year we measure Xn where n=100. I define Zj as the value of Xn on day j (= 1, 2, ..., m).

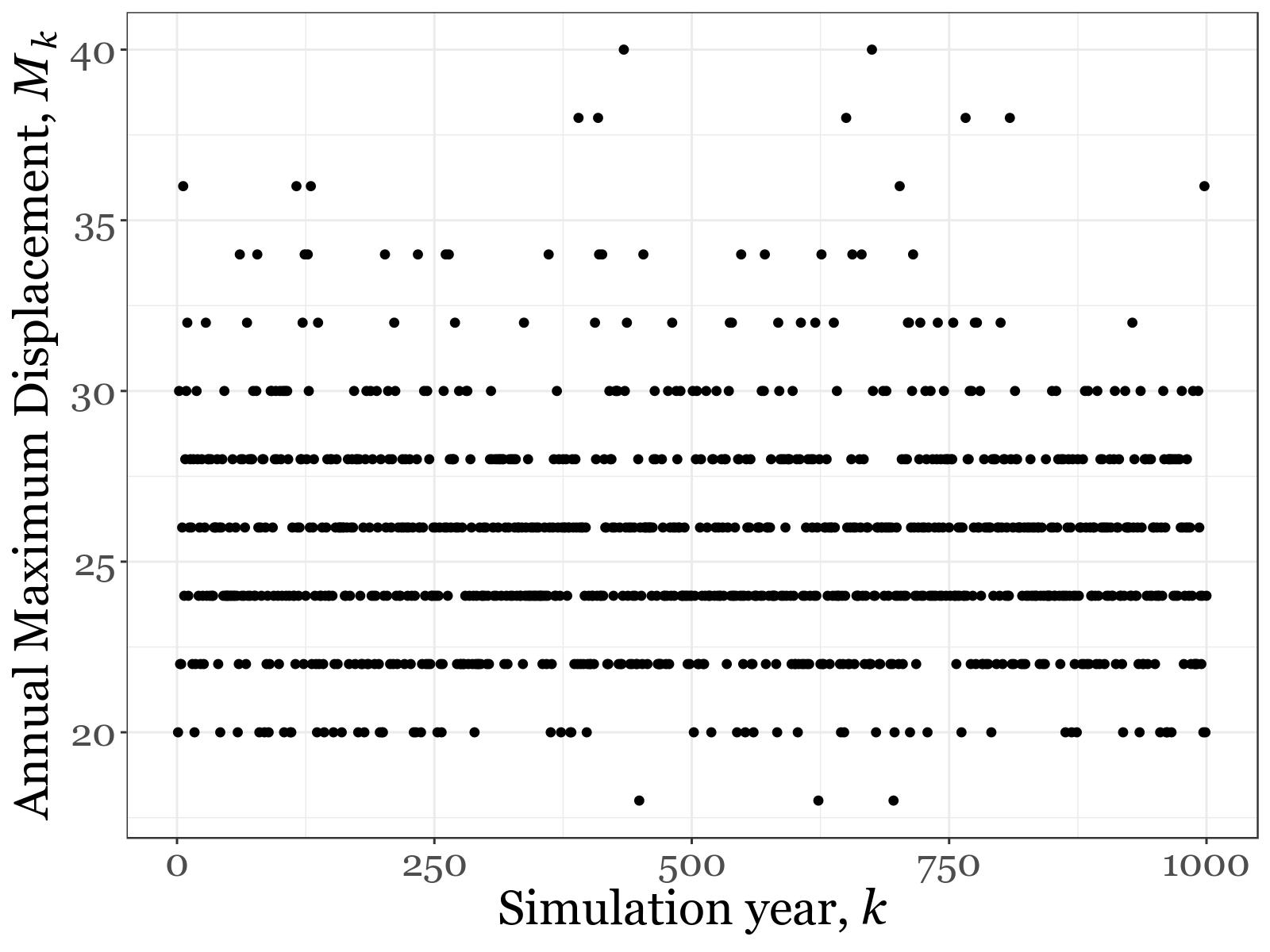
Figure 2 shows the daily displacement made by the drunk over a typical year. The points scatter about zero but on a few nights his displacement exceeded 20.
Daily Displacement Example
Fig. 2: The drunk's daily displacement over a given year.
The maximum daily displacement over a given year (k) is given by:

Mk = max{Z1, ..., Zm},

where m=365. The pub landlord wants to know the distribution of Mk, obtained by simulating the process over l years where l=1,000.
Annual Maximum Displacement over 1,000 years
Fig. 3: The drunk's annual maximum displacement over 1,000 years of simulations.
The pub landlord accepts the risk if the distance of the lake is greater than or equal to the 1% quantile of the distribution function:

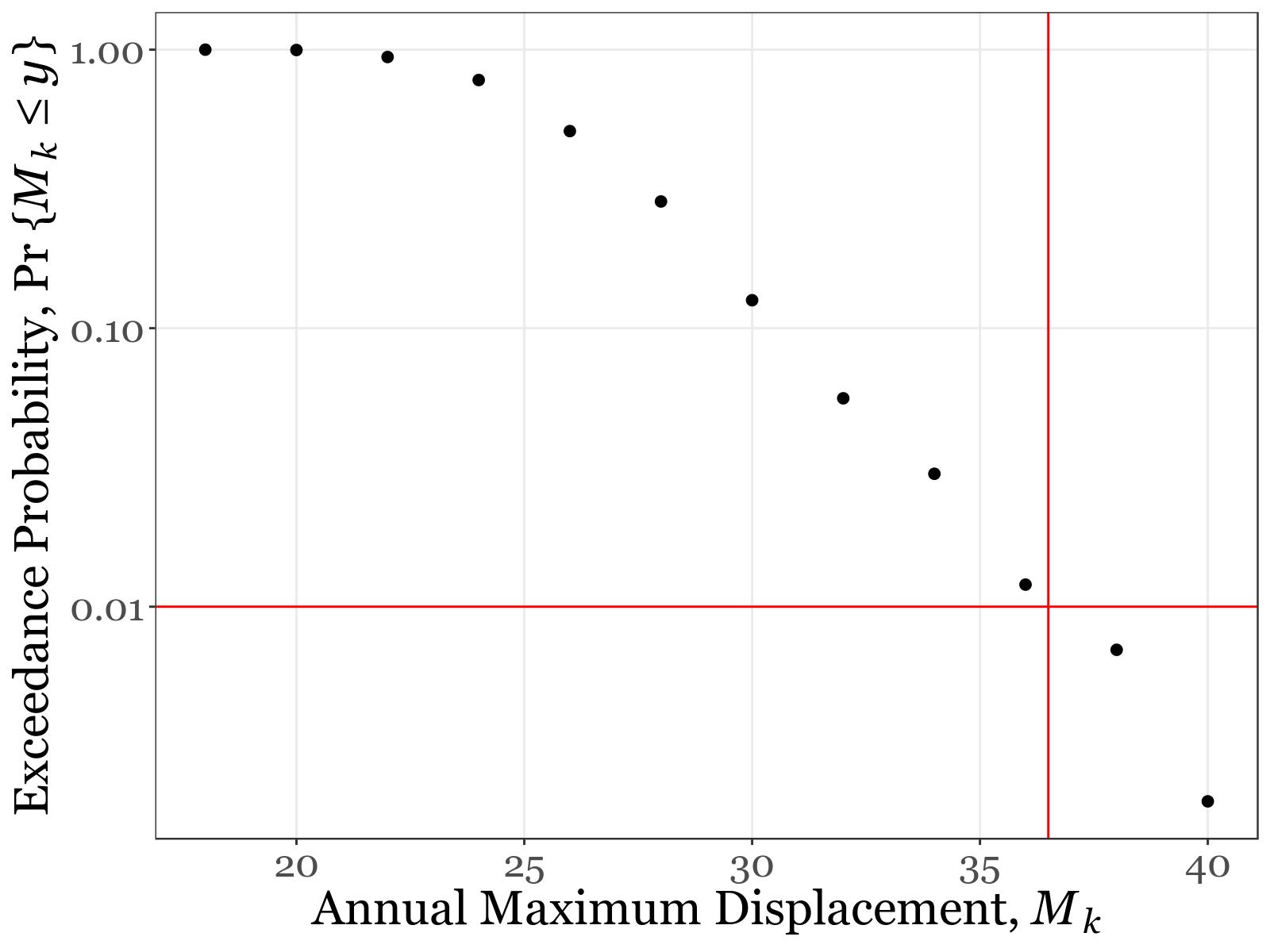
Pr{Mk ≤ y} = F(y).

1% implies that the drunk is likely to exceed this displacement once in 100 years, which is a greater duration that his life expectancy. Using Figure 4, the value of Mk which corresponds to an exceedance probability of 1% is about 36.5. As shown in Figure 1, the lake is 40 units from the drunk's home and therefore further away than the maximum displacement the drunk is likely to reach in his lifetime. The pub landlord can relax; it is extremely unlikely that his most regular customer will ever fall into the lake.
Exceedance Probability of Annual Maximum Displacement over 1,000 years
Fig. 4: Exceedance probability of the drunk's annual maximum displacement over 1,000 years of simulations. Red lines indicate the 1% quantile.

Alastair Clarke
10th November, 2018